TEL: 14 min. 42 seg.
¿Cómo puede tener el cosmos la entropía que observamos actualmente si la temperatura era casi exactamente la misma en todas partes luego del big bang? La respuesta podría radicar en nuestro "número telefónico cósmico", de acuerdo a Mag Tegmark.
En una charla, llamada "Encontrando el desafío de la entropía", que dio Tegmark en el Instituto de Tecnología de Massachusetts, el científico abordó una de las grandes preguntas de la cosmología actual:¿Cuál es la entropía, la cantidad de desorden, del universo? ¿Por qué la entropía es tan baja? ¿Y por qué es tan alta?
¿Si pudiéramos escribir una ecuación en una remera que describa todo el universo, qué información sería necesaria?

Lo que sigue es una transcripción de la charla, que puede además puede verse en el video adjunto.
Algunas aclaraciones previas:
La charla forma parte de un simposio en el que hubo otras charlas anteriores a la de Tegmark ese día. Es por eso que se alude a Charles Bennett (que dio la charla "La segunda ley y la física cuántica") y a Dick Bedeaux ("La segunda ley y la mecánica estadística").
Durante la charla, Tegmark utilizó diapositivas, por eso el lenguaje de la traducción tiene formas como "aquí vemos" o similares. Las diapositivas utilizadas por Tegmark pueden descargarse aquí.
Es perfectamente posible, al tener el video y la transcripción traducida al castellano, realizar directamente los subtítulos al video. Empero, eso infringiría los derechos de autor de MIT.
Por lo tanto, ilustro la nota con algunas imágenes para que directamente pueda ser leída (y entendida), aunque es viable leer el texto de la nota mientras se mira el video.
La charla se realizó en octubre de 2007, por eso, al aludir al "año anterior", se refiere a 2006, específicamente al señalar el Premio Nobel de Física para Matter y Smooth.
Finalmente, los enlaces en el texto fueron agregados míos, que creo pueden ser de ayuda para comprender algunos aspectos.
La transcripción original, en inglés, fue publicada en Arxiv, con el siguiente resumen:
Uso ejemplos de cosmología para ilustrar que la segunda ley de la termodinámica no está vieja, sino vivita y coleando, continuando a estimular interesantes investigaciones sobre los grandes enigmas. La pregunta "¿Por qué la entropía es tan baja?" (a pesar de la segunda ley) sugiere que nuestro universo observable es tan sólo una pequeña y casi uniforme región en un espacio vastamente mayor, estirado por la inflación cósmica. La pregunta "¿Por qué la entropía es tan alta" (comparada con la complejidad requerida para describir muchas candidatas a "teorías del todo") sugiere independientemente que la realidad física es mucho mayor que la parte que podemos observar.
[Presentación de Max Tegmark]
[APLAUSOS] Muchas gracias. Es un placer estar aquí. Me pidieron los organizadores hablar de la segunda ley y cosmología, y una reacción visceral para un título así es:"Espera un minuto - la segunda ley de termodinámica no tiene nada que ver con cosmología!". Cuando escuché por primera vez sobre la segunda ley, pensé que tenía más que ver con las Leyes de Murphy y la clase de física que tiene lugar en mi cocina, especialmente ahora con dos pequeños niños en las mañanas. Ustedes saben, los huevos se rompen y no se vuelven a armar. Y esta flecha local del tiempo que percibimos, ¿qué podría tener que ver con el universo?. Sin embargo, como vamos a ver, tiene todo que ver con el universo. De hecho, Dick Bedeaux y Charles Bennett mencionaron que la clave para entender nuestra flecha local del tiempo aquí es entender por qué empezamos en un estado inusual de baja entropía. Y entender cómo empezamos es, por supuesto, el negocio de la cosmología.

Así que, un poco más cuantitativamente, con una forma de contar, ¿Cuál es la entropía de nuestro universo observable, esta esfera en el espacio desde la cual la luz tuvo tiempo de llegar hasta aquí durante 13,7 mil millones de años desde el big bang? Esta entropía está en los 1089 bits. Hablando crudamente, un googol de bits. Mi charla tendrá dos partes. Hablaré de dos cuestiones:
1. ¿Por qué nuestra entropía es tan baja?
2. ¿Por qué nuestra entropía es tan alta?
Por la primera pregunta, significaré ¿por qué es que los 1089 bits es todavía mucho menor que el equilibrio térmico o qué significa eso?. Mucho menos que los 10122 bits que es el límite de Hawking y Bekenstein sobre cuánta entropía puede tener un volumen de este tamaño.
La segunda pregunta es ¿por qué en la Tierra es este número todavía mucho más grande que algo como cero? ¿De dónde vinieron todas estas complejidades?
Comencemos por la primera pregunta, "¿por qué la entropía es tan baja?", que, por supuesto, es crucial para entender nuestra flecha del tiempo. Primero debo decirles qué quiero decir con entropía. Me voy a apegar a la definición microscópica. Seguiré midiendo en bits, como hizo Charles Bennett, que pueden pensarlo como usando unidades donde la constante de Boltzmann es igual a 1. Hacia el final me voy a tomar algunas libertades y usar entropía casi sin rigor para referir al algoritmo de información o algoritmo de complejidad. Me voy a tomar estas libertades porque, francamente, tenemos severos problemas para incluso definir entropía en cosmología, que ustedes son bienvenidos en preguntar luego. Y como John von Neumann dijo una vez, nadie sabe qué es realmente la entropía, así que en un debate, ustedes siempre tendrán la ventaja.
Así que con estos cabildeos, ¿por qué la entropía es tan baja en nuestro sistema solar?. ¿Y cómo terminó nuestro sistema solar tan lejos del equilibrio térmico? La razón por la que tenemos vida aquí en este planeta, la fuerza que conduce la termodinámica detrás de la flecha del tiempo aquí, es que tenemos estos 6.000 Kelvin de luz solar radiando en nuestro planeta de 300 Kelvin, que a su vez radiando en un universo de 3 Kelvin. Este es el conductor número uno del proceso termodinámico que está ocurriendo aquí. ¿Cómo pudo llegar a esto? Si piensas en esto, es realmente llamativo. Hemos aprendido que cuando el universo era mucho más joven, la temperatura era casi exactamente la misma en todas partes. Comenzamos 400.000 años luego del big bang en una situación donde la densidad era casi perfectamente uniforme a través de nuestro universo observable, y la temperatura era casi exactamente la misma en todas partes dentro de una parte en 10-5. Este fue el tema del Premio Nobel de Física del último año para Mather y Smoot. Así que ¿cómo puedes tomar algo con casi la misma temperatura en todas partes y luego hacer algo realmente caliente aquí y otro tanto realmente frío?

Bien, veamos esta animación. Tenemos física clásica a la Boltzman donde tienes un puñado de átomos, que están comenzando a agruparse y terminan en una situación más uniforme. Esta es la forma usual en la que pensamos la segunda ley de termodinámica, tomar algo agrupado y hacerlo más uniforme. Bien, en cosmología, tiende a ser casi exactamente lo opuesto. Y la razón es la gravedad. Esto ocurre cuando no hay gravedad, mientras que cuando tenemos gravedad, si nos recordamos de lo que nos dijo Dick Bedeaux, cuando miramos este factor de Boltzman usual e-H/kT, el Hamiltoniano aquí contendrá un término de energía potencial de la gravedad, aquí en el exponente, que puede ser negativo. Y puede ser arbitrariamente negativo en gravedad clásica: si tomo dos partículas y las pongo arbitrariamente cerca una de otra, puedo tener una casi infinita energía negativa. Y lo que eso hace es darte una inestabilidad intrínseca, una inestabilidad termodinámica. Y como resultado, voy a mostrarles ahora, lo que realmente ha pasado en nuestro universo es que ha ido de ser casi uniforme a ser muy, muy agrupado.
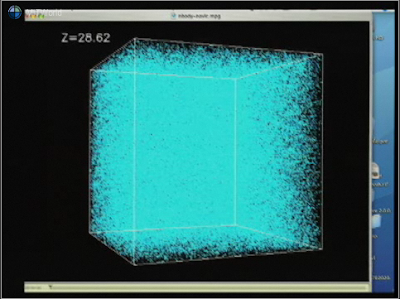

Déjenme hacer esto un poco más visual al mostrarles una simulación computacional de Ben Moore y su grupo en Zurich.
Lo que tenemos aquí es un cubo enormemente grande, muchos cientos de millones de años luz de lado, lleno con materia casi uniforme y todo lo que pusieron en este superordenador son las leyes de la gravedad. Cuando lo hacemos correr y vemos una casi uniforme distribución que se hace más agrupada. Una forma intuitivamente física de pensar acerca de porqué está pasando esto es que si empezaste con algo perfectamente simétrico y uniforme, por supuesto, por simetría debería mantenerse de esa forma. Pero si tienes un grupo aquí con un poco más de cosas que a su alrededor, luego ese agrupamiento atraerá gravitacionalmente más cosas de su entorno y se volverá más agrupado, lo que a su vez lo hace mejor para robar cosas de su entorno. El agrupamiento se hace más y más grande y antes de enterarte estas pequeñas sobre densidades de un nivel de 10-5 han crecido para formar galaxias, estrellas, planetas, etc. Básicamente, el rico se hace más rico. Eso es lo que la gravedad está haciendo aquí.
Así que acerquémonos a uno de estos agrupamientos, que tiene un tamaño como el del halo de materia oscura en el que vive nuestra galaxia Vía Láctea y veamos más ejemplos de la segunda ley en acción en cosmología. Esta es una simulación de supercomputadora ahora por Mattias Steinmetz y su grupo en Postdam, Alemania, donde pusieron, además de gravedad, la física básica de los gases. Lo que ven a la izquierda es una vista superior de lo mismo que ven en la derecha, visto de lado, que es gas gradualmente haciéndose más denso y más denso y formando estrellas y las cosas se están haciendo más y más desordenadas. Excepto, de nuevo, comparado con la forma en que usualmente pensamos en entropía incrementándose en un gas, haciéndose más uniforme, esto no se está haciendo más uniforme. Se está haciendo más y más agrupado y complicado. Y se dejas que esto ocurre mil millones de años, terminas con algo que se parece mucho a la galaxia Vía Láctea, que es nuestro hogar.
Si nos acercamos más cerca de casa ahora, en el entorno de sólo una de estas motas de luz aquí, sólo una estrella, podemos ver la segunda ley otra vez. Tenemos una nube de gas. Se contrae por la gravedad. Disipa e irradia mucha de su energía y se establece en un disco, y la contracción y agrupamiento continúa en el centro de esto hasta que el gas se hace tan denso que se incia la fusión nuclear en el núcleo de este agrupamiento y nace una estrella. Y mientras tanto, más alejados agrupamientos tuvieron lugar en las partes exteriores de este disco y una vez que la naciente estrella expulsa el gas residual, vemos estos agrupamientos que están formados aquí: planetas.
Comenzamos preguntándonos por qué la entropía es tan baja aquí en nuestro sistema solar: por qué tenemos temperaturas muy diferentes de distintos cuerpos celestes que nos permite tener vida aquí y así. La buena noticia es que la astrofísica ha realizado mucho progreso en esto, como las simulaciones computacionales ilustran, porque no ha sido puesta ninguna magia aquí: sólo pusimos la teoría de gravedad de Einstein y la física básica de gases y terminamos con lo que parece el universo que observamos.
Sin embargo, profundas cuestiones permanecen. ¿Por qué entonces fue que las cosas eran tan uniformes en el principio? Porque, como ya he dicho, eso realidad corresponde a la muy baja entropía en cosmología. ¿Por qué fue que el gas que llena nuestro universo observable fue tan uniforme como el gas en esta sala? El aire tiene fluctuaciones del nivel 10-5 por las ondas de sonido causadas por mi charla. ¿Por qué era tan uniforme en ese entonces? Y, además, ¿por qué es todo tan grande? ¿Por qué el espacio se está expandiendo? Hay un cúmulo de cuestiones que nos han hechizado por mucho tiempo. Y entonces nuestro colega Alan Guth, aquí en MIT, vino con una respuesta que sonaba completamente loca para esto, llamado inflación, que nos ha capturado como un fuego forestal y es ahora fuertemente apoyada por la observación. Su respuesta sobre por qué el universo empezó tan uniforme es que no lo hizo. En cambio, dijo que si tienes una pequeñísima región de espacio, mucho, mucho menor que un átomo, que por alguna razón es muy, muy uniforme y también muy, muy densa, luego este proceso de inflación puede expandir el espacio, como Einstein y Friedman mostraron hace tiempo que el espacio puede hacer, y expandirlo exponencialmente, y así doblar su tamaño una y otra vez, quizás cada 10-32 segundos, hasta que esta región subatómica de espacio se ha vuelto tan enorme que haz hecho todo el espacio en la parte del universo que podemos ver y más. Y lo hace todo uniforme. Así que en esta imagen, puedes comenzar con algo todo desordenado, quizás cerca de una clase de equilibrio termodinámico en un sentido vago, pero una pequeña parte de eso podría estirarse y volverse uniforme. Y como eso llena todo lo que podemos ver, nos engañamos pensando que todo era uniforme sólo porque arrogantemente nos gusta pensar que todo lo que podemos ver es todo lo que existe.
Esta es una idea que suena muy, muy loca, así que ¿por qué deberíamos creer una palabra de esto? Quiero recordarles que toda la cosmología fue vista con extrema sospecha a través de los sesenta y setenta. Fue considerada un tema muy excéntrico, en el borde entre metafísica y filosofía. Y sin embargo, la revista Science escribió este artículo en 2003, diciendo que el avance número uno del año es que ahora podemos comenzar a creer lo que estos cosmólogos están diciendo. ¿Y por qué escribieron eso? Lo escribieron porque hay datos. Como Bob Silbey mencionó, hemos disfrutado una revolución en las mediciones, en nuestra habilidad de cuantificar cosas allí fuera en el espacio. Y sólo para darles un ejemplo de esto, ya he hablado un poco de mapas de galaxias tridimensionales. Otro ejemplo son estas fotos de bebé del universo por las que George Smoot y John Mather ganaron el Premio Nobel el año pasado.
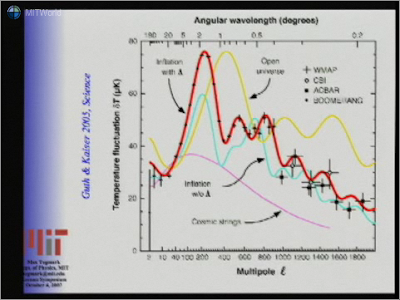
No se preocupen por lo que significan estos ejes. Lo que es importante es que las cruces negras aquí son mediciones con barras de error de un sigma, y la curva roja es una predicción teórica de la inflación. Esto está muy, muy lejos de los sesenta cuando podías especular acerca de cualquier cosa porque no había datos para probar que estabas equivocado. Se trata de un ajuste cuantitativo realmente impresionante. Y es por esta clase de mediciones que más y más personas están comenzando a pensar que Alan Guth también tendrá un viaje gratis a Estocolmo en algún momento. Porque esta teoría se está viendo muy creíble.
Así que hemos hablado acerca de porqué la entropía es tan baja. En otras palabras, porqué, al menos la parte de espacio en la que estamos está tan lejos del equilibrio térmico. Y déjenme usar mis restantes cinco minutos muy brevemente diciendo algunas palabras acerca de porqué la entropía es tan alta. Es un número enorme, 1089 bits. Ahora, ¿quién ordenó eso?[1]

Aquí en MIT, a mucha gente le gusta caminar con remeras con ecuaciones fundamentales en ellas. Y mis colegas en física teórica tienen su esperanza de Santo Grial que un día descubrirán no sólo algunas ecuaciones, sino las ecuaciones, para la teoría de todo. Nos darán una completa descripción del universo. Y lo que esperan particularmente es ser suficientemente elegantes para que esas ecuaciones entren en una remera, verdad? Esta puede ser una vana esperanza. Pero supongamos que sea cierta por un momento. Dejémonos entretener con ese pensamiento y veamos a dónde nos lleva. Luego, ¿cuánta de esta información es realmente necesaria en una remera? ¿Tiene que tener la remera una ecuación que tenga el número ocho en ella que diga que tenemos ocho planetas? De ninguna forma. Porque sabemos que hay muchos otros sistemas planetarios con tres planetas, dos planetas, cero planetas, y así, por lo que el número ocho sólo nos está diciendo algo sobre donde estamos viviendo, cierto?
¿Debe esa remera especificar todas las condiciones iniciales para nuestro universo observable? No. No debería, porque la inflación predice que el espacio no es sólo grande, sino realmente infinito. Así que si vas suficientemente lejos, por la clase de argumentos ergódicos que hemos escuchado esta mañana, toda clases de condiciones iniciales serán realizadas en alguna otra parte. Así que esas condiciones iniciales, que crean el conjunto de esos 1089 bits, sólo nos están diciendo dónde vivimos en el espacio. Esos 1089 bits sólo nos están diciendo nuestra dirección en el espacio. Así que no deberían ir en una camiseta, porque la remera describe todo el espacio, toda la teoría, verdad?

Y en la hermosa charla previa de Charles Bennett sobre física cuántica, supongan que toman un generador de números cuánticos aleatorio como su aparato Stern-Gerlach y empiezan a producir todo un puñado de números cuánticos aleatorios, ¿deberían esos números ir en la camiseta como algo fundamental acerca del universo? Bueno, si le dan a Charles Bennet una cantidad suficiente de cerveza, les confesará que él cree que la física cuántica es unitaria y seguramente, todos estos bits también nos están diciendo dónde estamos en este gran espacio cuántico de Hilbert donde estos diferentes resultados ocurren.
¿Qué debe ir en la remera entonces? Esto es de un reciente paper que escribí con mi colega Frank Wilczek aquí y Martin Rees y Anthony Aguirre: ustedes quisieran poner las 32 constantes sin dimensión de la naturaleza, que necesitamos para calcular todo, desde las masas de las partículas elementales hasta la fuerza de las interacciones y así. Eso podría ser una buena cosa para poner allí. Todavía no sabemos de dónde provienen. Realmente nos están diciendo algo acerca de nuestro universo. O quizás pongamos algunas ecuaciones, incluyendo el modelo estándar Langrangiano. Presiento que esta camiseta no sería muy viable financieramente. Pero quizás uno de ustedes vendrá con algunas ecuaciones más elegantes de la teoría de cuerdas o lo que sea, de lo cual esto sea sólo un caso especial. Pero incluso aquí hay un poco de sorpresa que viene de la teoría de cuerdas recientemente, que es que bien podría ser que en este espacio infinito incluso los valores de estas constantes podrían no ser completamente constantes a través de todo el espacio. Quizás sólo sean constantes en la gran porción que la inflación hizo. Y podría haber otros valores en algún otro lado, en cuyo caso incluso parte de esta información está sólo diciéndonos dónde vivimos. El punto clave que estoy haciendo es que la mayoría de la información que pensamos que describe algo fundamental acerca del universo podría ser solamente nuestra dirección, una forma de nuestro número telefónico cósmico.
Así que si se preguntan a ustedes mismos "¿es todo lo que observamos realmente todo lo que hay?", yo argumentaría que nuestra alta entropía, el hecho de que 1089 es un gran número, sugiere "no, hay probablemente más de lo que podemos ver". O poniéndolo de otra forma, si lo que podemos observar aquí requiere muchos más bits para describir que una descripción matemática completa del mundo para poner en una remera, luego estamos en alguna clase de multiverso o básicamente una realidad mucho mayor de la que podemos observar.
Para resumir, pienso que no sólo la segunda ley de la termodinámica tiene mucho que ver con cosmología, sino que da pistas intrigantes acerca de la futura investigación a seguir. ¿Por qué la entropía es tan baja? Probablemente porque ocurrió la inflación. ¿Por qué es tan alta? Estimo que es porque estamos en alguna clase de multiverso. ¿Sabemos esto? Absolutamente no. Pero mi punto clave es que estos son preguntas de investigación activa. Y si suena muy loco, pienso especialmente para los biólogos en la sala, debemos dar crédito a Charles Darwin aquí. Él nos dijo que hemos desarrollado la intuición como seres humanos para las cosas que tenían valor de supervivencia para nuestros ancestros, como la física clásica, las órbitas de las parabólicas de rocas en vuelo arrojadas hacia tí. Esa es la clase de cosas para las que esperamos tener intuición, nada más. Así que no es sorprendente que luego miremos a cosas muy pequeñas en el mundo cuántico y parezcan contra-intuitivas, cuando miramos cosas muy grandes, cosas muy veloces, agujeros negros, dilatación del tiempo, parece contra-intuitivo. Y pienso que si categóricamente rechazamos ideas y ciencia sólo porque se siente raro, probablemente rechacemos también la teoría correcta.
Finalmente, quisiera volver al principio antrópico que fue mencionado por Charles Bennett aquí. Ahora, la forma final de esto, la más extrema culinaria forma de esto, sería que, el universo debe ser uno que nos guste. Y el gran físico Richard Feynman tiene algo muy interesante que decir acerca de esto, con lo que quisiera terminar al mostrarles este video clip.
Feynman: Luego está el tipo de decir que usted no entiende el sentido de "yo no creo que ". Es muy loco. Es el tipo de cosas que estoy justo, no voy a aceptar". [...] Si usted desea saber la forma en que la naturaleza funciona, lo miramos con atención, mírelo - ver, esa es la forma lo que parece. Si no le gusta, ir a algún otro sitio! A otro universo donde las reglas son más simples, filosóficamente más agradables, psicológicamente más fáciles.
Así que concluyamos con algo que estoy seguros que estamos todos de acuerdo. Pienso que todos acordamos que a pesar de su vieja edad, la segunda ley no está vieja y cansada. En cambio, está viva y coleando. Y espero que estos ejemplos de cosmología hayan ayudado a ilustrar que la segunda ley de la termodinámica continúa estimulando verdadera investigación interesando sobre grandes, grandes acertijos. Gracias!.
Hasta aquí, los primeros 24 minutos de la charla (y del video), que se corresponden con 5 páginas y media de transcripción. La otra mitad es el debate, en el que los participantes pudieron realizar preguntas. Pondremos a disposición esa segunda parte aquí, muy pronto.
- Entropy and our cosmic telephone number
- The Second Law and Cosmology
- Video en MIT:The Second Law and Cosmology
Notas:
[1]:"¿Quién ordenó eso?", supongo que está parafraseando al físico teórico Isidor Rabi, del que se cuenta que se expresó de esa manera al enterarse de una nueva partícula descubierta, el muón.
 Sobre las imágenes
Sobre las imágenesLas imágenes son capturas de pantalla del video de la charla.
El video "The second law and cosmology" pertenece a MIT
 Astronomía en Blogalaxia-Cosmología-Ciencia en Bitácoras.com
Astronomía en Blogalaxia-Cosmología-Ciencia en Bitácoras.com

No hay comentarios.:
Publicar un comentario