T.E.L: 6 min. 38 seg.
Sobre los métodos de medición de distancias del universo son muy difundidos el uso de la paralaje trigonométrica, cefeidas y supernovas. Pero hay otros métodos que, en conjunto, forman una escalera de distancias.

En un post anterior, hablamos de las unidades de medida. Allí comentamos el uso de la paralaje trigonométrica. Y, al hablar de la Constante de Hubble, señalamos el uso de las supernovas y cefeidas como métodos para estimar distancias.
Sin embargo, hay muchos otros métodos usados. Muchas veces se los clasifica por ser absolutos o relativos. Los primeros son aquellos en los cuales se puede realizar una medición directa, mientras los segundos son aquellos basados en la existencia de tipos de objetos que tienen propiedades iguales entre sí (sea luminosidad o tamaño).
No se usa cualquier método para cualquier objeto, ya que cada técnica tiene sus limitaciones. Más bien se usan algunos métodos para calibrar otros, en una verdadera escalera de distancias cósmicas.
Para las medidas extragalácticas se suele decir que hay dos tipos de indicadores, nuevamente los primarios y los secundarios. Los primarios serían aquellos que pueden ser calibrados con nuestra galaxia o con alguna consideración teórica. Los secundarios son aquellos que usan distancias previamente establecidas con indicadores primarios.
Entre los indicadores primarios figuran la paralaje trigonométrica, el método de los cúmulos en movimiento (método del punto de convergencia), las estrellas variables cefeidas y RR-Lyrae y la paralaje espectroscópica.
Veamos algunos:
Indicadores primarios
Método del cúmulo móvil
Se piensa que las estrellas nacidas en un cúmulo abierto lo hicieron prácticamente al mismo tiempo de una misma nube molecular. Tienen, por tanto, la misma edad. Los astrónomos también piensan que estas estrelllas se mueven con el mismo vector velocidad. La distancia d al cúmulo se obtiene a partir de la velocidad radial v del cúmulo respecto a nosotros (por observaciones espectrales), el tamaño angular, y la variación de ese tamaño en un tiempo t:
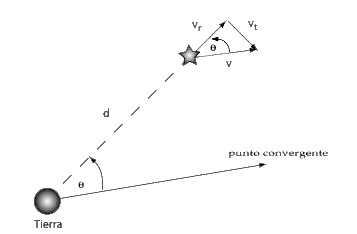
Así, con un grupo de estrellas físicamente relacionadas que comparten un movimiento, como las Hyades, y dado que por la perspectiva,los movimientos propios parecen estar dirigidos a un único punto, llamado punto de convergencia, si se conoce la velocidad líneal del cúmulo a partir de observaciones de la velocidad radial, puede estimarse la distancia de cada estrella a partir del movimiento propio total.
Más en: Método del cúmulo móvil
Cúmulo móvil en Wikipedia
Distances Measures for Open Star Clusters
En una reciente charla el físico Alberto Rojo señaló este método como un cruce entre la física y el arte, ya que utiliza el concepto de perspectiva, que tanto se ha utilizado en una y otra rama de la actividad humana.
Paralaje espectroscópica
Cuando no se conoce la paralaje a una estrella, se puede determinar su Magnitud Absoluta mediante el análisis del espectro, buscando efectos como el descubierto por la dupla Wilson-Bappu, y que lleva su nombre.
Uno de los primeros en formular un sistema para clasificar la luminosidad de la estrellas en función del diagrama H - R fueron W. W. Morgan, P. C. Keenan y E. Kellman, en el año 1943. Posteriormente, en 1962, fue perfeccionado por Morgan y Keenan en lo que se conoce como Sistema MK.
La idea es que algunas estrellas tienen características específicas en sus espectros, que permiten calcular su magnitud absoluta y, por lo tanto, su distancia. Por ejemplo, la línea de absorción K del calcio, que es ancha y alcanza un máximo en estrellas K0.
una vez que tengamos el tipo espectral y la clase de luminosidad de una estrella podemos calcular su magnitud absoluta y, por lo tanto, su distancia. Éste es el método de paralaje espectroscópico.
Más en Paralaje espectroscópico
Paralaje espectroscópia en Astrocosmo
Ajuste al diagrama de Hertzsprung-Russell
La estrellas se pueden clasificar en un diagrama de Hertzsprung-Russell. El diagrama se encuentra en luminosidades o magnitudes absolutas, mientras que nosotros observamos la magnitud aparente de las estrellas.
El método consiste en ajustar la distancia promedio para todas las estrellas que hace que la distribución se ajuste al diagrama.
Para los cúmulos remotos, los paralajes no pueden ser medidos pero los espectros de sus estrellas se pueden utilizar para obtener el diagrama HR. Tal diagrama es un diagrama de magnitud aparente contra tipo espectral. Si comparamos este diagrama con el diagrama HR calibrado por las Híades, encontramos que los dos son idénticos a excepción de la escala vertical. La diferencia entre la magnitud absoluta y aparente determina la distancia del cúmulo lejano.
Un gráfico de magnitud aparente en función del índice de color para un cúmulo abierto estaría desplazado respecto a un diagrama HR. El desplazamiento de la secuencia principal del gráfico de magnitud aparente en función del índice de color respecto de la secuencia principal del diagrama HR es el módulo de la distancia, por lo tanto midiendo este desplazamiento, se puede determinar la distancia al cúmulo. Este método fue desarrollado por H.L.Johnson.
El módulo de distancia es la diferencia entre la magnitud aparente m, corregida de la absorción estelar y su magnitud absoluta M de un objeto. Está relacionada con su distancia d (expresada en parsecs) según la relación:
Más en Ajuste del Diagrama HR
Determinación de la distancia al cúmulo abierto NGC 3532 por el método de superposición de secuencias principales por L. Ciocci Brazzano; G. Acuña
en Informes especiales de Física Recreativa.
Métodos secundarios
La relación V4 para galaxias espirales y elípticas
La relación de Tully-Fisher
Fue publicada por los astrónomos R. Brent Tully y J. Richard Fisher en 1977 y permite estimar la distancia a la que se encuentra una galaxia espiral a partir de la anchura de las líneas de su espectro.
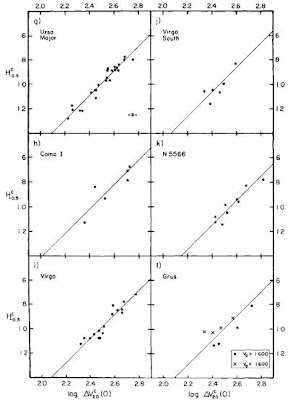
La relación, derivada de forma empírica, establece que la luminosidad de una galaxia espiral es proporcional a la cuarta potencia de su velocidad máxima de rotación que, a su vez, se determina a partir de la anchura de las líneas espectrales, en particular de la línea a 21cm emitida por el hidrógeno neutro de la galaxia. Conocida la luminosidad L es posible determinar la distancia d por comparación entre la primera y la magnitud aparente m.
La relación de Tully-Fischer se calibra con galaxias cercanas en las que se conoce la distancia a partir de Cefeidas.
Las mejores bandas para medir el brillo de las galaxias son las infrarrojas, pues:
El efecto de la extinción por polvo interno y externo a las galaxias es menor y
representan mejor a la masa de las poblaciones estelares (bandas azules muy influenciadas por formación estelar reciente).
Más en Relación Tully-Fisher
Relación TF en Wikipedia
Relación Faber-Jackson
Relación entre la Luminosidad de una galaxia elíptica y su dispersión de velocidades para el cálculo de su distancia descubierta por Sandra Faber y Roger Jackson. Fue luego mejorada con la relación D-Sigma:
En las galaxias elípticas existen también relaciones entre su tamaño, velocidad de dispersión y luminosidad. Cuanto mayor es la luminosidad de una elíptica, mayor es la dispersión de velocidad.
Las Cefeidas no se encuentran en las elípticas, y por tanto necesitan otros métodos de medida de distancia para calibrar la relación.
Suele usarse para determinar distancias a cúmulos, promediando las medidas obtenidas para cada galaxia elíptica de éste.
Más en: Relación Faber-Jackson en Wikipedia
D-Sigma: Mejora a la relación FJ
Método de fluctuación de brillo superficial
En 1988, John L. Tonry y Donald P. Schneider propusieron utilizar la fluctuación del brillo superficial de una galaxia como nuevo medio de determinar su distancia. La idea detrás del método es que, aunque un telescopio puede no resolver una población de estrellas brillantes en una galaxia lejana ausente, la naturaleza discreta de las estrellas causa fluctuaciones en el brillo superficial de la galaxia. El grado de estas fluctuaciones disminuyendo con la distancia, la apariencia de una galaxia se vuelve entonces más suave conforme se incrementa la distancia.
Más en Método de fluctuación de brillo
Funciones de luminosidad
Se pueden usar también los objetos más brillantes de una galaxia. Para esto se pueden usar las super gigantes rojas, los cúmulos globulares, o las regiones HII gigantes. Para esto los astrónomos usan la función de luminosidad de un cúmulo globular de una galaxia, por ejemplo, y la comparan con las magnitudes relativa y absoluta.
La función de luminosidad promedio de los cúmulos globulares en torno a la Vía Láctea, la Gran Nube de Magallanes y M31 parecen ser la misma. Es posible suponer, por tanto, que lo mismo ocurre en otras galaxias.
Así los astrónomos pueden usar la función de luminosidad promedio de los cúmulos globulares como una candela estándar que permite calcular la distancia a su galaxia padre.
Más en Objeto más brillante en una galaxia
Efecto Sunyaev-Zel'dovich
El efecto Sunyaev-Zeldovich (efecto SZ) es el resultado de la interacción de la radiación de fondo, con electrones libres a una temperatura mayor. Fue propuesto por los investigadores Rashid Sunyaev y Yakov Zel'dovich en 1968. Esta interacción se da en las grandes estructuras del universo como los supercúmulos o cúmulos galácticos. Teniendo como resultado neto un corrimiento al azul en el espectro del Fondo cósmico de microondas.
Más en entrevista con Matthias Bartelmann en IAC y en Efecto Sunyaev-Zeldovich de Lucia Guaita.
Las lentes gravitatorias también ayudan
El retraso temporal en las fluctuaciones de luz observadas en las múltiples imágenes de un cuásar producidas por un cúmulo de galaxias puede proporcionar una escala de distancias. El sistema mejor estudiado hasta ahora es el cuasar QSO 0957+561, con el que se ha determinado un valor de la constante de Hubble de 70 km/s/Mpc.
Más en La Bella Teoría y en Nueva Estimación de la Constante de Hubble.
La escalera
Estos distintos métodos y otros aquí no mencionados conforman lo que se denomina escalera cósmica de distancias. En la Enciclopedia de la ciencia de David Darling se ilustra con la siguiente imagen (editada):

Y he aquí otra ilustración de la escalera (de Cosmología Observacional de Beatriz Granados):

Más en: Comparación de los diferentes métodos
Nota escrita para el VIII Carnaval de la física, en esta edición hospedado por Pirulo cósmico. Para unirse y leer las entradas existe una red social en Ning.
Fuentes y links relacionados
- Una fuente de referencia permanente para esta entrada fue el curso de astrofísica en internet del Dr. Victor Migenes y el Dr. Roger Coziol.
- Cosmologia observacional: Medidas de distancias cosmologicas de Beatriz Ruiz Granados PDF)
- La escala de distancias y expansión del Universo, de José A. de Diego
Sobre las imágenes
- Imagen adaptada de la que figura en la Enciclopedia de la ciencia en internet, de David Darling (cosmic distance ladder).
- Relaciones de Tully-Fisher infrarrojas para grupos cercanos de galaxias.(Aaronson & Mould 1983, ApJ, 265, 1) de Enciclopedia de astrofísica en internet.
- Imagen principal: Combinación de imagen de escalera de blikdsgn (http://www.sxc.hu/) con imagen de Hubble/NASA de NGC 1850.
Etiquetas:
Astronomía en Blogalaxia-Ciencia en Bitácoras.com


No hay comentarios.:
Publicar un comentario