CdlF: Unidades de longitud en astronomía

T.E.L: 6 min. 36 seg.

Un repaso por las unidades básicas que utilizan los astrónomos para medir las distancias en el universo es nuestro aporte al II Carnaval de la Física.

Los científicos usan las unidades rutinariamente. Entre las más usuales figuran el Año luz, el parsec y la unidad astronómica.

Medidas estandarizadas
El Sistema Internacional de Unidades (SI) define siete unidades básicas o unidades físicas fundamentales, de las que se derivan las demás.
La longitud es una magnitud escalar cuya unidad básica es el metro (m) que, desde 1983, se define como la distancia que viaja la luz en el vacío en 1/299.792.458 segundos.
Podemos utilizar múltiplos del metro para expresar distancias mayores o menores. Para las mayores, podemos usar desde el kilómetro (10³ metros) hasta el yottametro (10²⁴).

La Unidad Astronómica
La Unión Astronómica Internacional es responsable de mantener y aprobar un conjunto especial de unidades en astronomía, definidas formalmente en 1976. Una de las más importantes es la Unidad astronómica (UA), que es definida por la UAI como el equivalente a la distancia desde el centro del Sol al cual una partícula de masa infinitesimal, en una órbitra circular sin perturbaciones tendría un período orbital de 365,2568983 días. Es, por tanto, la distancia promedio entre la Tierra y el Sol, de casi 150 millones de kilómetros (149.597.870 km; 1,49·10¹¹ m)
Originalmente la UA había sido definida como la longitud del semi eje mayor de la órbita elíptica de la Tierra alrededor del Sol. En 1976, la UAI revisó la definición para tener mayor precisión: radio de una órbita circular newtoniana alrededor del Sol de una partícula con masa infinitesimal con un movimiento medio de 0,017 202 098 95 radianes por día (constante gravitacional de Gauss).
Esta definición da cuenta de los estudios de Kepler (su tercera ley), de la reformulación de Newton y de los cálculos de Gauss.

Ahora bien, recientemente contamos sobre un llamado de atención que un investigador realizó sobre esta unidad de longitud. Es que la constante gravitacional de Gauss está relacionada con la masa del Sol y el astro pierde masa permanentemente. Lo contamos en "Proponen redefinir la Unidad Astronómica".

El Parsec
Más allá del Sistema Solar la distancias son tan grandes que usar la UA se vuelve incómodo. Para los estudios de la estructura de la Vía Láctea se usa el parsec.
El parsec es equivalente a 3,09×10¹³ km (unas 206.265 UA, o 3,26 años luz). Se define como la distancia a la que una Unidad Astronómica subtiende un ángulo de un segundo de arco.
El término proviene de parallax of one arc second, o paralaje de un segundo de arco. Por lo tanto, para entender qué es un parsec, debemos saber primero qué es la paralaje.

La paralaje
Se llama así a la desviación aparente de la posición de un objeto, según desde el lugar que se lo observe. Normalmente se la define como: Ángulo formado por la dirección de dos líneas visuales relativas a la observación de un mismo objeto desde dos puntos distintos, suficientemente alejados entre sí y no alineados con él. En español el término es femenino.
Hay diferentes clases de paralajes, como anual, horizontal, solar, lunar y la trigonométrica. Esta última se define como el ángulo bajo el cual se ve el radio de la órbita de la Tierra, desde una estrella a una distancia normalizada de una unidad astronómica. Se expresa en segundos de arco: En un círculo que está dividido en 360 grados (360º), cada grado está dividido en 60 minutos (60'), también llamados "minutos de arco" para distinguirlos de los minutos de tiempo y cada minuto contiene 60 segundos de arco (60")
Como vemos, para estimar un parsec debemos partir de la definición de UA. La distancia a la estrella es el inverso de la paralaje trigonométrica expresado en parsec.

Para establecer la paralaje a una estrella, la observamos en un momento del año y luego a los seis meses (cuando la Tierra dio media vuelta al Sol y está en el lugar opuesto de la órbita).
En ambas observaciones veremos una posición aparente de la estrella, ligeramente distinta de la real. Pero al combinar las dos observaciones podremos establecer el ángulo de las dos líneas visuales. Y conocemos la distancia de la Tierra al Sol. Con estos datos podemos usar la trigonometría para derivar la distancia a la estrella.

Desde la Tierra, medimos el ángulo P que subtiende este cambio de posición.
Obtenido este dato, dada la geometría de la situación, obtenemos que el paralaje corresponde a la mitad de P. Ahora que tenemos P podemos despejar D, que es a la distancia entre el Sol y el objeto requerido. Asumiendo que conocemos la distancia Tierra-Sol d (igual a 1 UA), utilizamos la trigonometría, ya que hemos construido un triángulo rectángulo y:

Por último, si deseamos la distancia D en parsecs, debemos transformar P a segundos de arco, y aplicamos la fórmula:

Para ser más claros podemos usar una animación interactiva llamada Stellar parallax interactive:

Allí no podremos calcular nada, pero sí notar si hay alguna diferencia entre la visualización de una estrella en un momento y en otro. Veremos a la Tierra orbitando alrededor del Sol. Podremos establecer la distancia de nuestro planeta al Sol y la distancia de nuestro astro a la estrella. Probemos, por ejemplo, con una órbita terrestre máxima y una distancia a la estrella mínima. Detenemos la animación en dos momentos, cuando el planeta está en lugares opuestos de la órbita, digamos en julio y, en el recuadro superior derecho veríamos una diferencia, un "movimiento" en la estrella más brillante:

y en enero y veríamos esto otro:

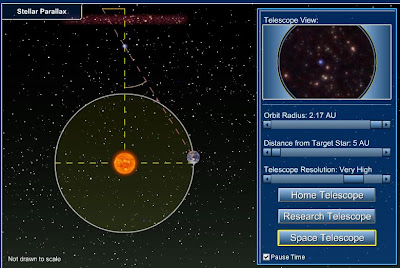
Ahora repitamos el procedimiento pero estableciendo la distancia Tierra-Sol en 1 UA y dejamos la distancia a la estrella igual (5 UA)
Y veríamos esto:

y esto:

Podemos cambiar la resolución del telescopio también y repetir el procedimiento.

Ejercicio: Proxima Centauri se encuentra a 1,31 pc ¿Cuál es su paralaje?
De la ecuación D=d/p, conocemos D y queremos saber p, despejamos p y la ecuación queda p=d/D => p=1/1,31 => p=0,765 arcseg.

Si no sabemos la distancia a la estrella, pero sí medimos su paralaje:
D=d/p => D=1/0,765 => D=1,31 pc

Ejercicio 2:
ESA lanzará el satélite Gaia capaz de medir la paralaje de estrellas a 180.000 años luz de distancia. ¿Qué ángulo será capaz de medir el satélite?
Pasamos los años luz a parsec:
Si 3,26 AL = 1 pc, luego,
180.000 AL/3,26 pc = 55.214 pc

P=d/D
P=1/55.214
P=0,000018 segundos de arco!!

Podemos visualizar otra animación, esta vez de Gaia, para entender la paralaje.

El Año Luz
La unidad de medida más usual de encontrar en la literatura de difusión, artículos periodísticos y obras de ciencia ficción es el año luz. Se trata, contrario a lo que puede parecer a simple vista, de una medida de longitud y no de tiempo. Es la distancia que recorre la luz en un año. Sin embargo, el tiempo se inmiscuye aquí, ya que decimos "en un año", que es en un año Juliano (365,25 días de 86.400 segundos). El año juliano es el tiempo que tarda la Tierra en orbitar al Sol.
Para mayor precisión, es la distancia que recorrería un fotón en el vacío a una distancia infinita de cualquier campo gravitacional o campo magnético, en un año Juliano. Esta definición tiene en cuenta que la luz puede ser desviada por un campo gravitacional, como el de una estrella, por ejemplo.
Un año luz es equivalente a 9,46 × 10¹² km, es decir, casi diez billones de metros (ó 9,46 x 10¹⁵ m).

En algunos trabajos científicos podemos encontrar referencias a Kly, Mly o Gly: El kilo año luz equivale a 1.000 años luz ó 306,6 parsecs y se usa para medir distancia entre partes de una galaxia.
El mega año luz es un millón de años luz, 306.600 parsecs y se usa para medir distancias entre galaxias vecinas y cúmulos de galaxias.
El giga año luz equivale a mil millones de años luz (306,6 millones de parsecs). Es una de las medidas más grandes usadas típicamente para estructuras supergalácticas como los cuásares.

Algunas equivalencias
1 pc = 3,0857 × 10¹⁶ m.
1 pc = 3,26 años luz.
kiloparsec (kpc): mil parsecs, 3.260 años luz.
megaparsec (Mpc): un millón de parsecs, 3,26 millones de años luz.
1 AL = 63.241 ua
1 AL = 0,3066 pc

Nota: lo cierto es que todas estas medidas son aproximadas, por lo que todas ellas debieran estar antecedidas por el símbolo "~".

Existen varias herramientas online para convertir unidades de medida, por ejemplo en Convertworld.com.

¿Spat?
El Diccionario de Distancias (*1) indica el uso del Terametro (10¹² metros), unidad que antiguamente se conociera como Spat, equivalente a 6,6846 UA. El origen no está claro del término Spat, pero podría haber sido como acrónimo de "Space Unit", o Unidad de Espacio. (*2).

El almanaque astronómico
En El almanaque astronómico es un almanaque publicado por el Observatorio Naval de los Estados Unidos. En su página podemos encontrar pdfs con algunas constantes astronómicas seleccionadas.

Un descanso para programar
Los astrónomos construyen sus propios programas de computación para analizar y filtrar los datos generados por los instrumentos y generar modelos, visualizaciones, etc. En esos programas usualmente deben convertir unidades de medida y utilizar los estándares estipulados para las distintas magnitudes (no sólo la longitud).
IAU creó una librería de algoritmos para establecer y mantener un conjunto de constantes y procedimientos para uso de los profesionales. Se llama SOFA (Standards Of Fundamental Astronomy) y contiene una variedad de rutinas que permiten facilitar la creación de programas en los lenguajes Fortran y C.

Fuentes y links relacionados