T.E.L: 6 min. 9 seg.
¿Por qué los astrónomos proponen que existe "materia oscura"? Un interactivo nos ayuda a comprender esto, interactuar y realizar ejercicios. Añado el video de una charla TED sobre el tema.
La llamada "Materia oscura" atrae la atención de las personas comunes y corrientes, como de los astrónomos.
Pero ¿qué es eso? Para que el público general pueda al menos tener una idea de a qué se llama materia oscura hay un buen recurso interactivo para que nos pongamos en la piel de un astrónomo que estudia la galaxia y la materia que contiene. Para eso habrá que observar y entender las interacciones que se producen entre este material.
El interactivo, de McGraw-Hill, cuenta con una introducción para entender la cuestión básica, una explicación de cómo usar el interactivo, una serie de ejercicios para terminar de comprender el tema y las resoluciones de los ejercicios propuestos.
Como todo está en inglés, traduzco aquí todo, excepto el interactivo mismo. Para completar, podemos leer La historia de la materia oscura.
Lo que encontraremos aquí es básicamente que la respuesta a ¿qué es la materia oscura? es, en realidad, otra pregunta o varias. Los astrónomos no saben a ciencia cierta qué es, por lo cual intentan descifrar el misterio con experimentos como el AMS que está a punto de partir hacia la Estación Espacial Internacional.
Introducción
En 1687 Isaac Newton explicó su Ley de la Gravitación Universal en su libro "Philosophiae Naturalis Principia Mathematica". Declaró que la fuerza gravitacional entre dos objetos depende del producto de sus masas y la inversa del cuadrado de la distancia entre ellos. Los científicos alrededor del mundo probaron la teoría de Newton por años, en laboratorios de la superficie Terrestre y a través de las observaciones de cuerpos en el sistema solar. En nuestro Sistema Solar, por ejemplo, el Sol contiene casi toda la masa y los planetas orbitan a su alrededor. La teoría de Newton predice que los planetas cercanos al Sol (como Mercurio) deben orbitan más rápidamente, mientras los más lejanos (como Plutón) deben moverse más lentamente. Y eso es exactamente lo que las observaciones mostraron.
En las décadas de 1970 y 1980, los desarrollos en astronomía volvieron a traer la cuestión de la gravedad a consideración. Mediciones de la velocidad a la que las estrellas y el gas orbitaban en las partes exteriores de la galaxia -"curvas de rotación"- no tenían sentido. Fotografías de galaxias mostraron que la mayoría de su luz, y por lo tanto la mayoría de sus estrellas, estaba concentrada cerca del centro. Eso implicaba que la mayoría de la masa de las galaxias también estaba concentrada cerca del centro. Así como el Sistema Solar, que tiene casi toda su masa concentrada en el Sol, las galaxias concentran la mayoría de su masa en el centro. Al igual que los planetas interiores orbitan más rápidamente que los exteriores, las estrellas cerca del centro de las galaxias deberían moverse más rápidamente que las más alejadas, pensaron los astrónomos. Pero las mediciones indicaron que la velocidad orbital de las estrellas era casi la misma, sin importar cuán lejos del centro estuvieran.
¿Cómo es esto posible? Una forma de explicar el problema fue postular que las galaxias contienen no sólo las estrellas y gas que podemos observar, sino grandes cantidades de material que no podemos ver: la llamada "materia oscura". Si esa materia está dispersa casi en forma regular a través de una galaxia, luego las estrellas lejos del centro "sentirán" el tirón gravitacional de no sólo el material central, sino toda la otra materia entre ellas y el centro. La fuerza extra debida a la "materia oscura" puede acelerarlas a casi la misma velocidad que las estrellas cercanas al centro.
Este interactivo le permite variar la cantidad de materia oscura en una galaxia y ver cómo afecta la velocidad orbital de las estrellas. Otra forma de verlo es que la fuerza gravitacional extra de la materia oscura es necesaria para mantener las estrellas en sus rápidas órbitas en las partes exteriores de la galaxia.
Pestaña "Cómo funciona el interactivo"
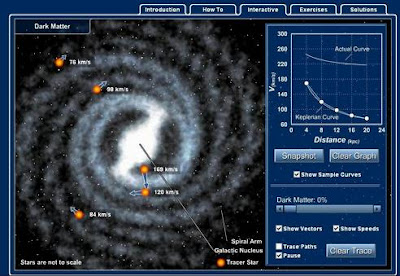
Al comenzar el interactivo veremos una panel principal a la izquierda con una visión de una galaxia espiral desde arriba. Orbitando alrededor de la galaxia hay cinco estrellas representativas, mostradas en naranja. Las estrellas circulan alrededor de la galaxia debido a la fuerza gravitacional que la materia en sus órbitas ejerce sobre ellas. Si pulsamos la caja "Show Speeds" ("Mostrar velocidades"), una etiqueta aparecerá cerca de cada estrella indicando su velocidad orbital.
En la esquina superior derecha hay un gráfico que ilustra la velocidad orbital (en el eje vertical) como una función de la distancia desde el centro de la galaxia (en el eje horizontal). Los astrónomos llaman a este gráfico la "curva de rotación" de una galaxia. Si pulsamos el botón "Snapshot", aparecerá un marcador para cada estrella. El botón "Clear Graph" ("Borrar Gráfico") borra todos los marcadores.
 La primera imagen del post es una captura de pantalla del interactivo, sin materia oscura. En este otro caso, con 50% de materia oscura.
La primera imagen del post es una captura de pantalla del interactivo, sin materia oscura. En este otro caso, con 50% de materia oscura.En la esquina inferior derecha de la pantalla hay un panel de control. El deslizador "Dark Matter" añade material a la galaxia en una forma especial. Cuando está en cero, la única materia en la galaxia está en sus estrella y gas. Podremos ver que la mayoría de las estrellas y gas están cerca del centro, así que la mayoría de la masa está concentrada allí también. Si incrementamos el valor del deslizador, añadimos materia oscura de manera relativamente uniforme en la galaxia, un poco cerca del centro, algo en el medio, algo cerca de los límites. Notar que 100% de Materia Oscura significa que habrá tanta materia de esa clase como materia normal.
La caja "Show Vectors" ("Mostrar vectores") muestra las velocidades en forma gráfica, con vectores: cuando mayor sea la flecha, más rápido se está moviendo la estrella. Podemos detener la acción con el botón "Pause".
Notar que al pulsar "Show Sample Curves" ("Mostrar curvas de muestra") trae dos curvas en el gráfico que ilustran los dos extremos de velocidad rotacional constante y velocidad de rotación debida a una masa central.
En la esquina inferior derecha hay también una opción llamada Trace Paths que al elegirla mostrará con puntos la órbita que siguen las estrellas.
Ir al interactivo sobre Materia Oscura
Ejercicios
1-Establecer el deslizador de Materia Oscura a cero. Tomar una imagen "Snapshot" de los movimientos. ¿Qué forma tienen los puntos en el diagrama de la esquina superior derecha?
2-¿Cuán rápido se mueve la estrella más cercana al centro y cuál es su distancia al centro?
3-¿Cuán lejos del centro está la siguiente estrella más cercana al centro? ¿Cuán rápido se mueve?
4-La Ley de la Gravitación Universal de Newton dice que, para sistemas en los cuales toda la masa está concentrada cerca del centro, las velocidades orbitales deberían decrecer con el cuadrado de la distancia. Esto es, si doblamos la distancia, la velocidad debería caer a 1/raíz cuadrada de su valor original. ¿Los datos que obtuvimos antes, siguen esta relación?
5-Pulsemos el indicador "Show Speeds" para mostrar las velocidades. Incrementemos el deslizador de materia oscura al 50%. Eso añade 50% de materia extra a la masa de la galaxia, dispersada de manera uniforme. ¿Cuál es la velocidad de la estrella más cercana al centro ahora? ¿Cuál es la velocidad de la siguiente estrella cercana?
6-Estas velocidades, ¿obedecen ahora a la relación 1/raíz cuadrada?
7-Graficar (con el botón Snapshot) la curva de rotación. Describir cómo cambia el patrón del gráfico.
8-Hagamos el mismo ejercicio, con las velocidades mostradas, pero con la materia oscura al 100% y anotemos la velocidad de las dos estrellas más cercanas al centro.
9-Volvamos a graficar y ver qué gráfico obtenemos ¿cuál es el diseño ahora?
Respuestas:
1-Vemos una curva que baja hacia la derecha, de forma un tanto abrupta al principio y menos luego lejos del centro. A medida que la distancia (ilustrada en kpc) aumenta, la velocidad (km/s) decrece.

2-La estrella más cercana al centro tiene una velocidad de 169 km/s y se encuentra a 4 kpc (lo vemos claramente en el gráfico).
3-La siguiente estrella más cercana está a 8 kpc y se mueve a 120 km/s.
4- Veamos: 169 km/s * (1/raíz(2))=119,5.
Sí, cuando sólo hay materia visible presente, las dinámicas estelares siguen las leyes de Newton.
Nota=¿Por qué hace "raíz(2)"?
5-Con 50% de materia oscura la estrella más cercana al centro (que sigue a 4 kpc) se mueve a 225 km/s y la siguiente a 200 km/s.
6-Esta vez, 225 km/s * (1/raíz(2))=160 km/s. Por lo tanto, no, la siguiente estrella más cercana se está moviendo más rápido (200 km/s) que lo que la relación predice. ¿Por qué? Porque algo de la materia oscura que añadimos cae entre la estrella más interior y la siguiente. Esa materia no afecta el movimiento de la estrella interior, pero brinda una fuerza adicional a la siguiente estrella.

7-El diseño de los puntos en el gráfico está ahora menos curvado y las velocidades son mayores.
8-Con el 100% de materia oscura (que significa que hay tanta materia de esa clase como de materia normal), las dos estrellas se mueven a 280 km/s.
9-El gráfico muestra una línea plana todas las estrellas se mueven a la misma velocidad.

¿Por qué hace "raíz (2)"?
Veamos:
La Ley de la inversa del cuadrado se aplica en la Ley de gravedad de Newton.
¿Qué es esa ley? Justamente la inversa del cuadrado. Puede ser más simple de entender si primero sabemos cómo calcular una proporcionalidad al cuadrado. Así será simple luego comprender qué implica la inversa.
Tomemos dos variables cuyos valores desconocemos, no importan. Pero sabemos que si el valor de x aumenta, el de y lo hará en relación al cuadrado del aumento de x.
Así, si cuando x=1, y=4; entonces cuando x=4, y=42=16.
Pongamos como ejemplo la superficie de una esfera, que se calcula:
4*PI*r2, donde r es el radio.
Veamos el cuadro 1: Refleja el radio de una esfera y su superficie, calculada con la fórmula antes indicada.
Con la fórmula es fácil calcular cuál será la superficie para una esfera de distintos radios: 4, 8, etc.

Ahora imaginemos que no sabemos la fórmula, pero sí sabemos que la superficie es proporcional al cuadrado y sabemos también la superficie para el radio 1.
Entonces, mantenemos la proporción y llegamos al mismo resultado, sin conocer la fórmula:
Cuando el radio aumenta en 4, la superficie deberá ser 42, respecto de la de radio 1;
Cuando el radio aumenta en 8, la superficie deberá ser 82, respecto de la de radio 1; etc.
Ahora volvamos a las estrellas del interactivo.
Si usamos el mismo, sin materia oscura, los valores, si existiera proporcionalidad al cuadrado (no inversa), serían:

En cambio, son los que siguen:

Vemos en el cuadro 3 que, en vez de calcular la proporción como la distancia al cuadrado, lo hacemos con la raíz cuadrada, que es la operación inversa.
Al hacerlo, los valores en vez de crecer, decrecerán.
Para saber la velocidad a 4 kpc de distancia, multiplicamos la velocidad a 1 kpc por 1 sobre la raíz cuadrada de la distancia (4). Así, 1/raíz(4) es 1/2 (0,5).
De la misma forma:
1/raíz(8)=0,35; 1/raíz(12)=0,29; etc.
Llegado este punto y viendo el cuadro 3, Ud. podrá notar que no estoy haciendo en ningún caso raíz(2), sino raíz(4); raíz(8); etc.
¿Por qué entonces en la respuesta anterior se usó raíz(2)?
Porque en los tres primeros cuadros, los cálculos como se puede apreciar se realizan en relación al valor de 1. En el cuadro 3, se mantiene el valor de 1 (que es 338) para calcular el resto. Por eso marqué en negrita al decir "respecto de la de radio 1".
Pero ¿qué pasa si no sé cuánto vale la velocidad para la distancia de 1 kpc?
Bueno, no es muy difícil. Podemos hacer dos cosas:
a-Lo que hizo el autor del interactivo, que fue:
En vez de hacer 1/raíz(dist), es decir 1 sobre raíz de la distancia; lo que hizo fue 1/raíz(dist/dist.ant), es decir, 1 sobre raíz de la distancia dividido por la distancia anterior.
Tomemos las filas dos y tres del cuadro 4:
Sé que a 4 kpc, la velocidad es 169 km/s. ¿A cuánto será la velocidad para 8 kpc?
8/4=2
169*(1/raíz(2))=120, que fue lo que hizo el autor del interactivo en la respuesta correspondiente.

b.Pero también podemos hacer lo siguiente: calculamos el valor para 1 y luego hacemos lo mismo que en los tres primeros cuadros:
Si seguimos la idea del punto a, entonces podemos deducir lo que valdría la velocidad para la distancia de 1 kpc, así:
x, es la velocidad a 1 kpc, es decir, la incógnita:
x*(1/raíz(distancia/distancia anterior))=169
x*(1/raíz(4/1))=169
x*(1/raíz(4))=169
x*(1/2)=169
x=169*2
x=338
Si ya sé que una estrella a 1 kpc tendrá una velocidad de 338 km/s y sé que la proporción es inversa del cuadrado de la distancia, entonces puedo hacer lo mismo que en el cuadro 1, es decir, mantener la proporción sobre el valor de la unidad, que es lo que se ve en el cuadro 3.
Veamos:
La Ley de la inversa del cuadrado se aplica en la Ley de gravedad de Newton.
¿Qué es esa ley? Justamente la inversa del cuadrado. Puede ser más simple de entender si primero sabemos cómo calcular una proporcionalidad al cuadrado. Así será simple luego comprender qué implica la inversa.
Tomemos dos variables cuyos valores desconocemos, no importan. Pero sabemos que si el valor de x aumenta, el de y lo hará en relación al cuadrado del aumento de x.
Así, si cuando x=1, y=4; entonces cuando x=4, y=42=16.
Pongamos como ejemplo la superficie de una esfera, que se calcula:
4*PI*r2, donde r es el radio.
Veamos el cuadro 1: Refleja el radio de una esfera y su superficie, calculada con la fórmula antes indicada.
Con la fórmula es fácil calcular cuál será la superficie para una esfera de distintos radios: 4, 8, etc.

Ahora imaginemos que no sabemos la fórmula, pero sí sabemos que la superficie es proporcional al cuadrado y sabemos también la superficie para el radio 1.
Entonces, mantenemos la proporción y llegamos al mismo resultado, sin conocer la fórmula:
Cuando el radio aumenta en 4, la superficie deberá ser 42, respecto de la de radio 1;
Cuando el radio aumenta en 8, la superficie deberá ser 82, respecto de la de radio 1; etc.
Ahora volvamos a las estrellas del interactivo.
Si usamos el mismo, sin materia oscura, los valores, si existiera proporcionalidad al cuadrado (no inversa), serían:

En cambio, son los que siguen:

Vemos en el cuadro 3 que, en vez de calcular la proporción como la distancia al cuadrado, lo hacemos con la raíz cuadrada, que es la operación inversa.
Al hacerlo, los valores en vez de crecer, decrecerán.
Para saber la velocidad a 4 kpc de distancia, multiplicamos la velocidad a 1 kpc por 1 sobre la raíz cuadrada de la distancia (4). Así, 1/raíz(4) es 1/2 (0,5).
De la misma forma:
1/raíz(8)=0,35; 1/raíz(12)=0,29; etc.
Llegado este punto y viendo el cuadro 3, Ud. podrá notar que no estoy haciendo en ningún caso raíz(2), sino raíz(4); raíz(8); etc.
¿Por qué entonces en la respuesta anterior se usó raíz(2)?
Porque en los tres primeros cuadros, los cálculos como se puede apreciar se realizan en relación al valor de 1. En el cuadro 3, se mantiene el valor de 1 (que es 338) para calcular el resto. Por eso marqué en negrita al decir "respecto de la de radio 1".
Pero ¿qué pasa si no sé cuánto vale la velocidad para la distancia de 1 kpc?
Bueno, no es muy difícil. Podemos hacer dos cosas:
a-Lo que hizo el autor del interactivo, que fue:
En vez de hacer 1/raíz(dist), es decir 1 sobre raíz de la distancia; lo que hizo fue 1/raíz(dist/dist.ant), es decir, 1 sobre raíz de la distancia dividido por la distancia anterior.
Tomemos las filas dos y tres del cuadro 4:
Sé que a 4 kpc, la velocidad es 169 km/s. ¿A cuánto será la velocidad para 8 kpc?
8/4=2
169*(1/raíz(2))=120, que fue lo que hizo el autor del interactivo en la respuesta correspondiente.

b.Pero también podemos hacer lo siguiente: calculamos el valor para 1 y luego hacemos lo mismo que en los tres primeros cuadros:
Si seguimos la idea del punto a, entonces podemos deducir lo que valdría la velocidad para la distancia de 1 kpc, así:
x, es la velocidad a 1 kpc, es decir, la incógnita:
x*(1/raíz(distancia/distancia anterior))=169
x*(1/raíz(4/1))=169
x*(1/raíz(4))=169
x*(1/2)=169
x=169*2
x=338
Si ya sé que una estrella a 1 kpc tendrá una velocidad de 338 km/s y sé que la proporción es inversa del cuadrado de la distancia, entonces puedo hacer lo mismo que en el cuadro 1, es decir, mantener la proporción sobre el valor de la unidad, que es lo que se ve en el cuadro 3.
Para completar más el tema, añadimos un video de una charla TED, que posee subtítulo en español, de Patricia Burchat.
http://www.ted.com/
Nota escrita para el X Carnaval de la física, en esta edición hospedado por Cienciamia. Para unirse y leer las entradas existe una red social en Ning.
Fuentes y links relacionados
- Playing with Dark Matter, por Adam Frank.
Sobre las imágenes
- Capturas de pantalla del interactivo. Crédito: McGraw-Hill.
Etiquetas:
Astronomía en Blogalaxia-Ciencia en Bitácoras.com


No hay comentarios.:
Publicar un comentario